细说如何完美实现macOS中的神奇效果

前言

神奇效果运行时，窗口的底部先逐渐收窄，收窄到一定程度后，窗口开始向下吸收。

底部收窄

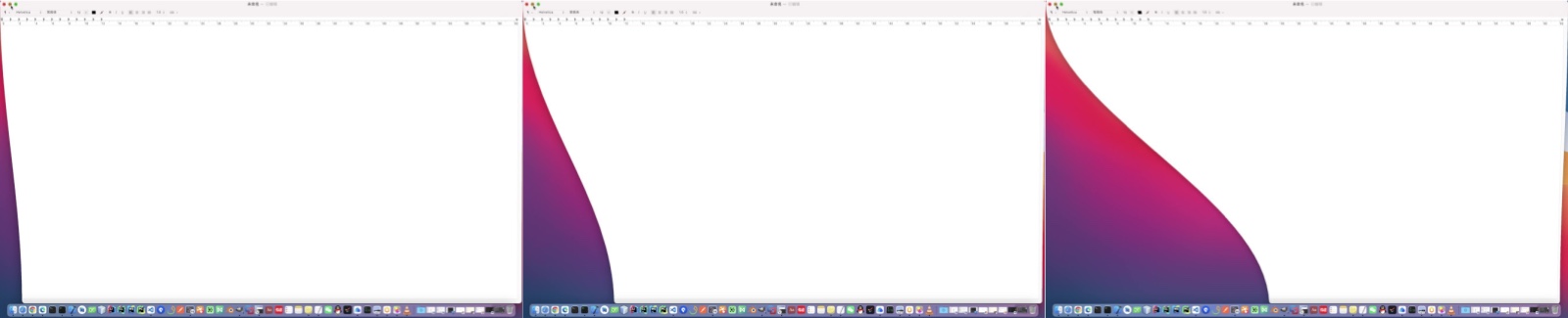
在这个过程中，左右两侧会出现曲线，随着时间的推移，曲线的形变程度越来越大，直到最终停止形变。窗口始终被限制在两侧曲线之间。

向下吸收

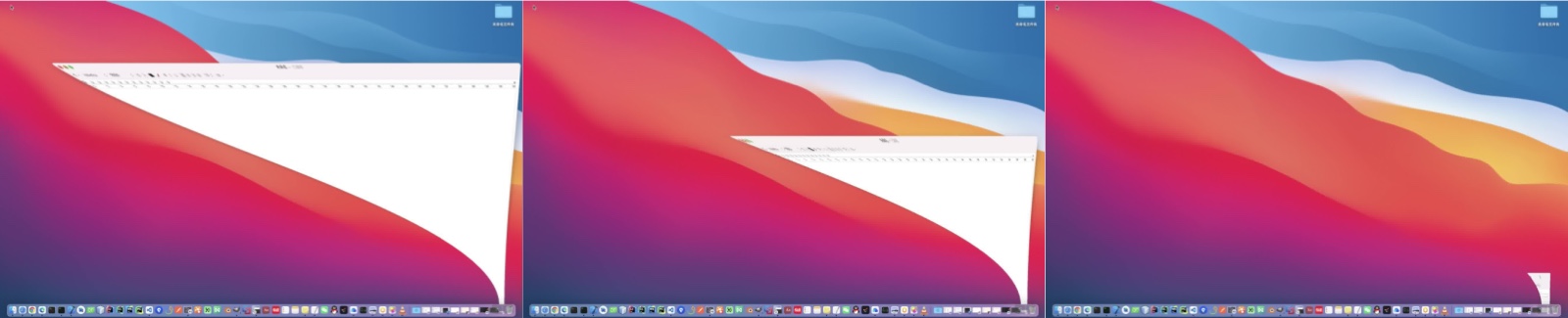
在这个过程中，窗口向下进行运动，逐渐消失。和底部收窄一样，窗口也是始终被限制在两侧曲线之间。

剖析

底部收窄的过程，是两侧曲线的演变过程。两侧的曲线可以用正弦曲线或余弦曲线表示。这里只拿正弦曲线进行说明。

周期函数回顾

先回顾一下在中学时期所学的周期函数，对于A * sin(B * (x + C)) + D来说，可以得出以下信息：

• 振幅为A
• 周期为2π / B
• 相移为−C
• 垂直移位为D
• 值域为[D - A, D + A]

根据上面的内容，对于值域为[MIN, MAX]的周期函数，我们很容易得到以下公式：

• D - A = MIN
• D + A = MAX

sin(x)的曲线：

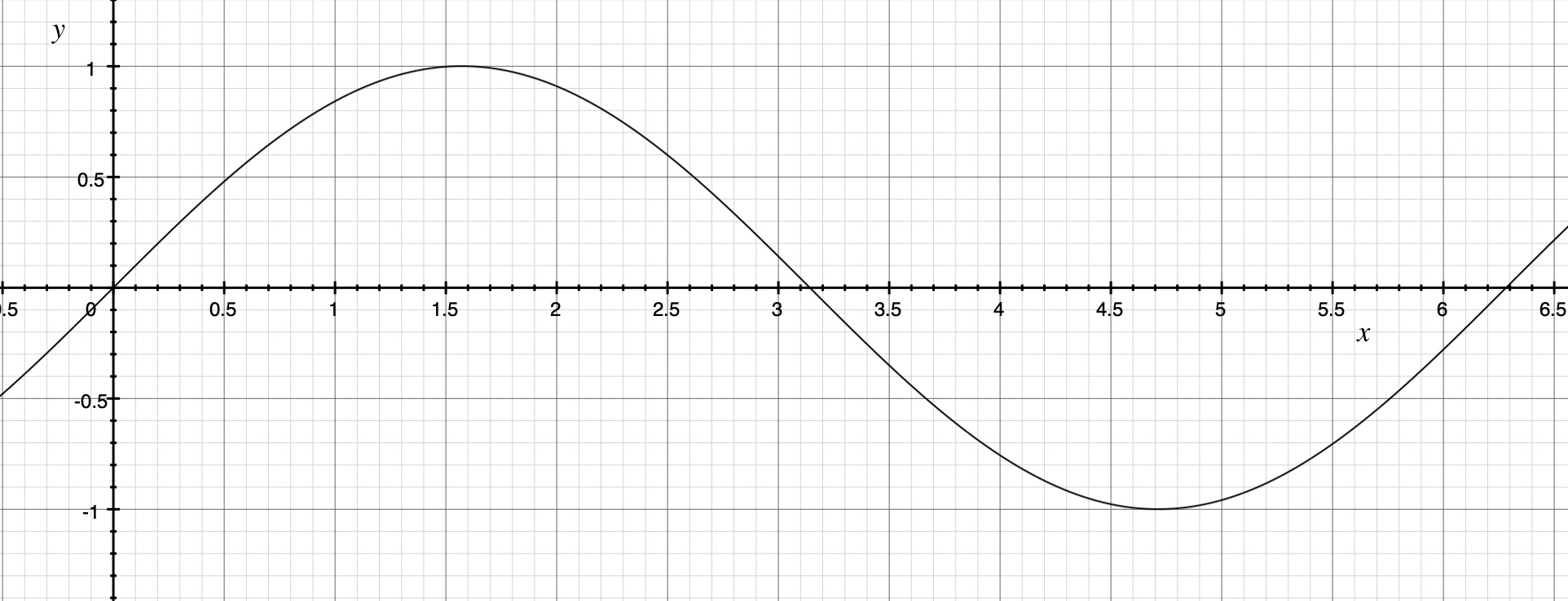
推导所需周期函数

为了方便理解，先把神奇效果放到坐标系中，这里使用纹理坐标。

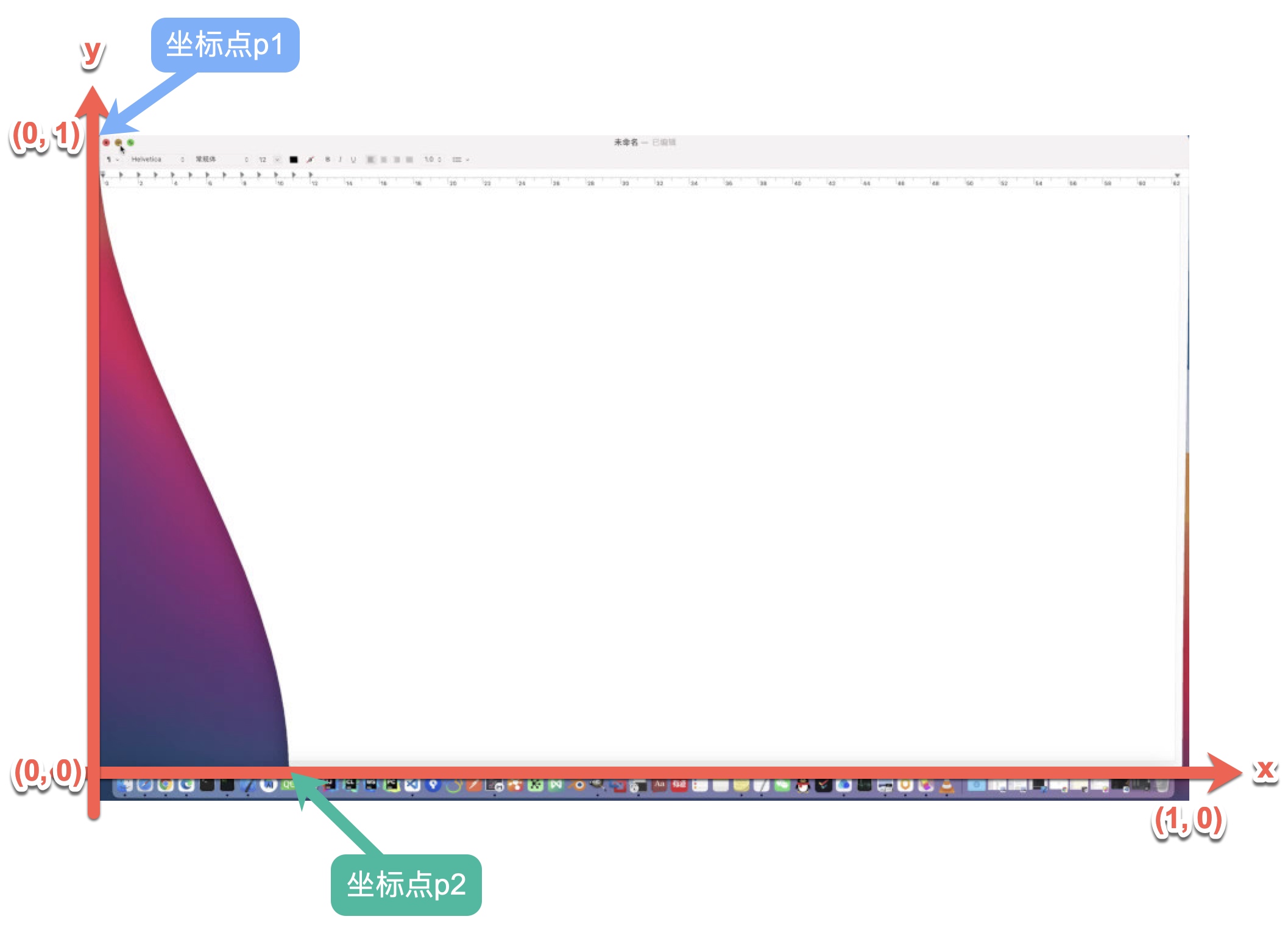
很明显，p1和p2这两个点的x坐标值就是曲线在x轴上的最小值与最大值。为了让曲线不断演变，就需要将p1点的位置固定在(0, 1)，而让p2点的x坐标一直向右移动，其y坐标保持为0，也就是说，我们需要通过这两个点的x坐标值（对应周期函数值域的最小值与最大值），得到对应的曲线。

可以看出：

1. x从最小值变成最大值的过程中，y只改变了1
2. y为0时，曲线的x值最大
3. y为1时，曲线的x值最小

因此，我们所需要的是一个周期为2（最小值变成最大值，需要半个周期）、相移为-0.5（周期除以4，然后减去对称轴的x，最后取负）、值域最小值为0的周期函数（此时的A和D相同）：

A * sin(π * x + π * 0.5) + A或D * sin(π * x + π * 0.5) + D

比如：

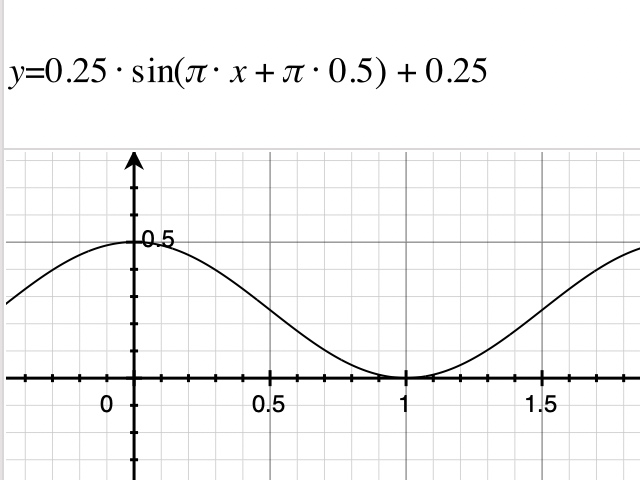
当然，上面得到的函数，其y值是根据x值的变化而变化的，而神奇效果中使用的函数，其x值是根据y值的变化而变化的（当然，也可以将程序坞放置到左侧或右侧，这样就是y值根据x值的变化而变化）。

修改一下周期函数，将x修改为y：

A * sin(π * y + π * 0.5) + A或D * sin(π * y + π * 0.5) + D

然后，可以得到类似这样的曲线：

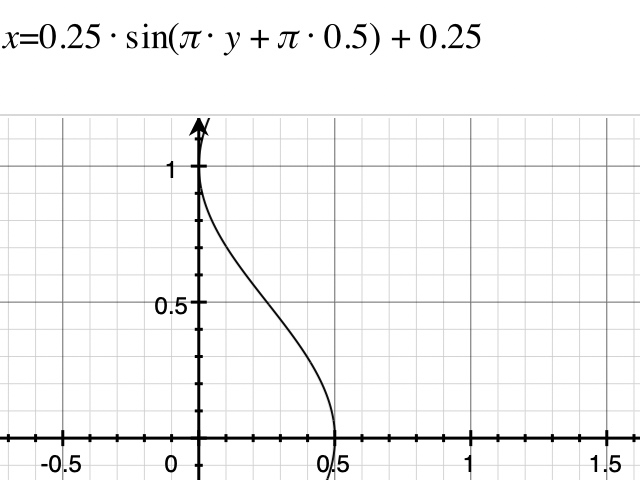
当使用不同的值域最大值（也就是D + A，因为此时的A和D相同，最大值也是2 * D或2 * A）时，可以得到不同的曲线：

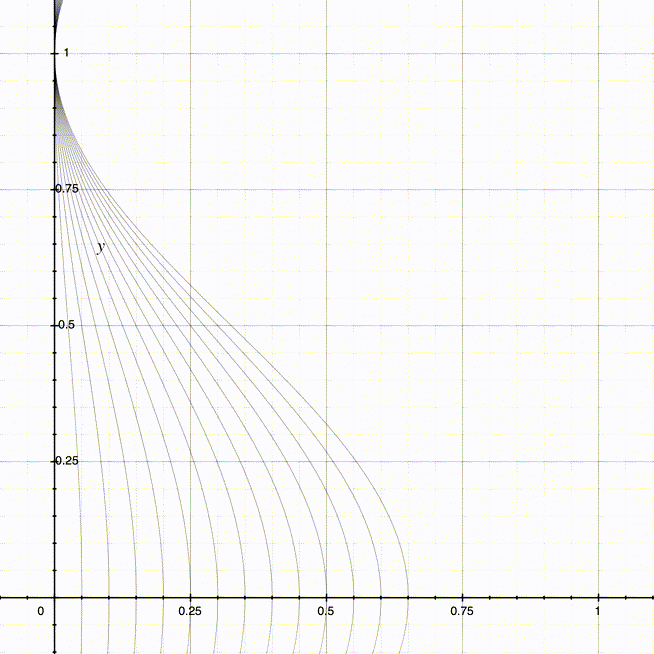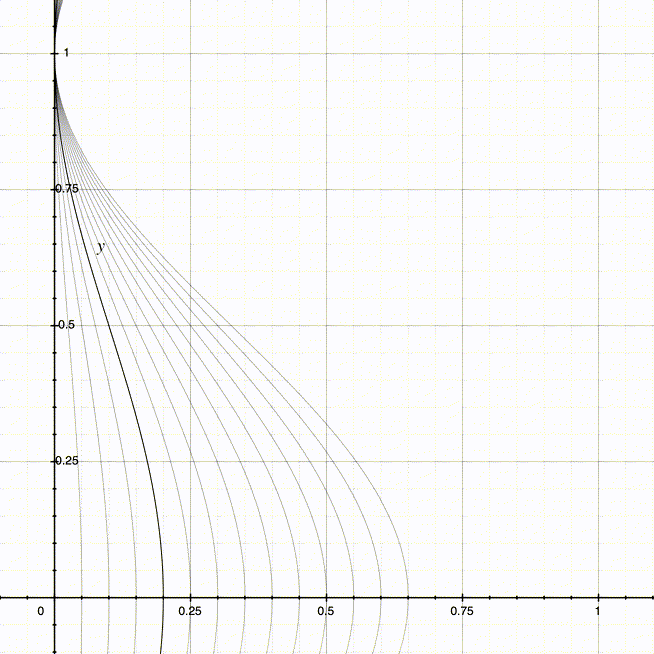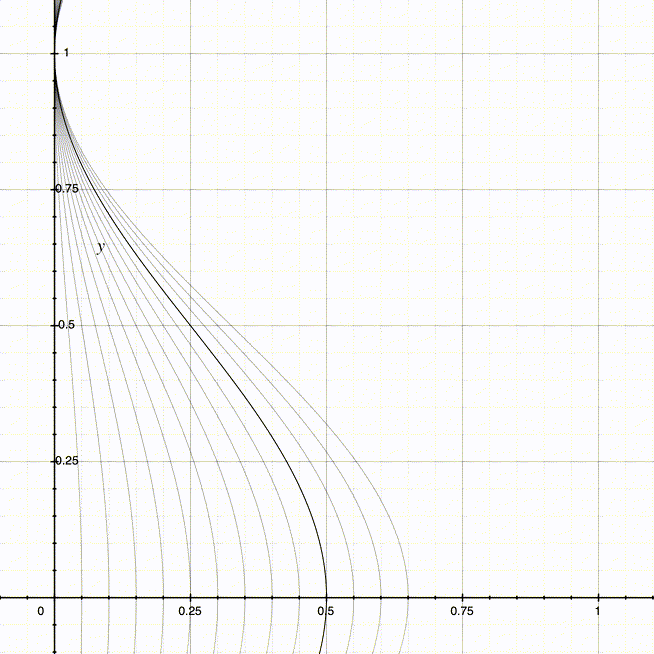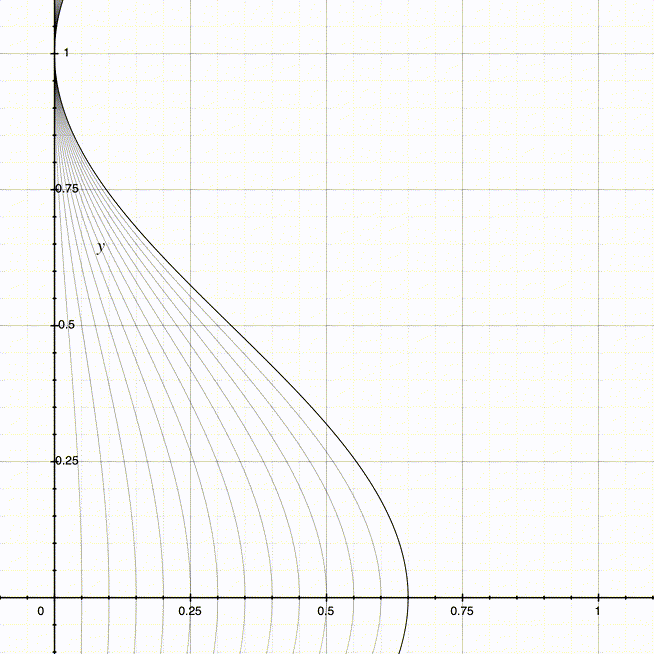
同理，我们可以得到右侧曲线所对应的周期函数：

A * sin(π * y - π * 0.5) + D

此时，D + A = 1。当使用不同的值域最小值（也就是D - A）时，也可以得到不同的曲线：

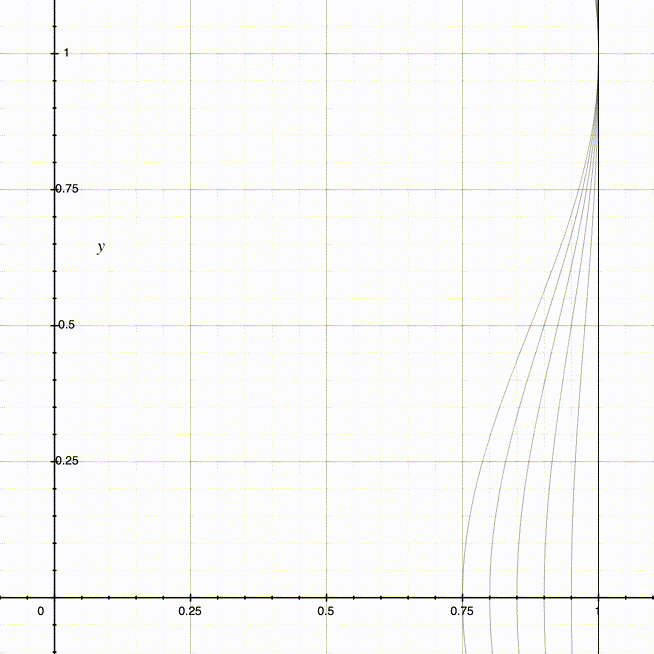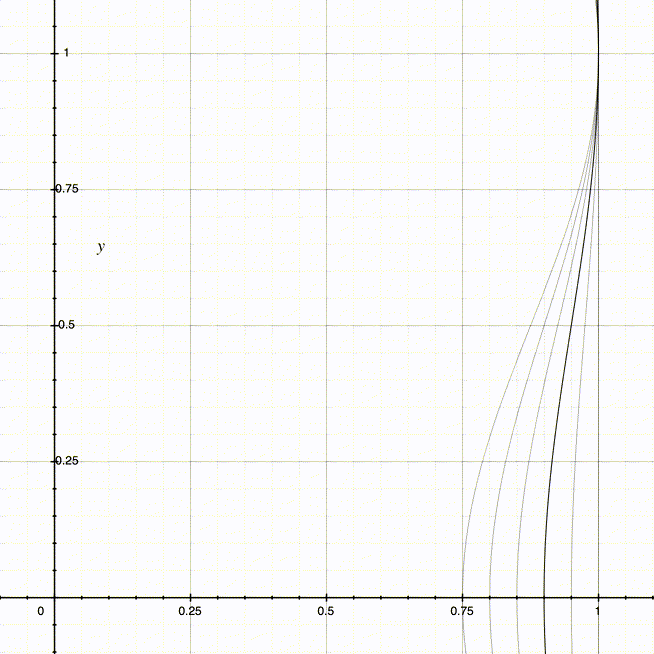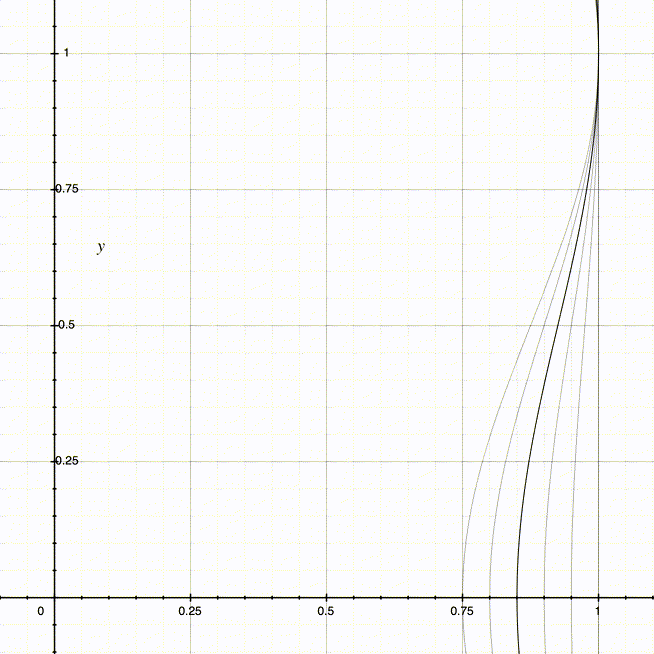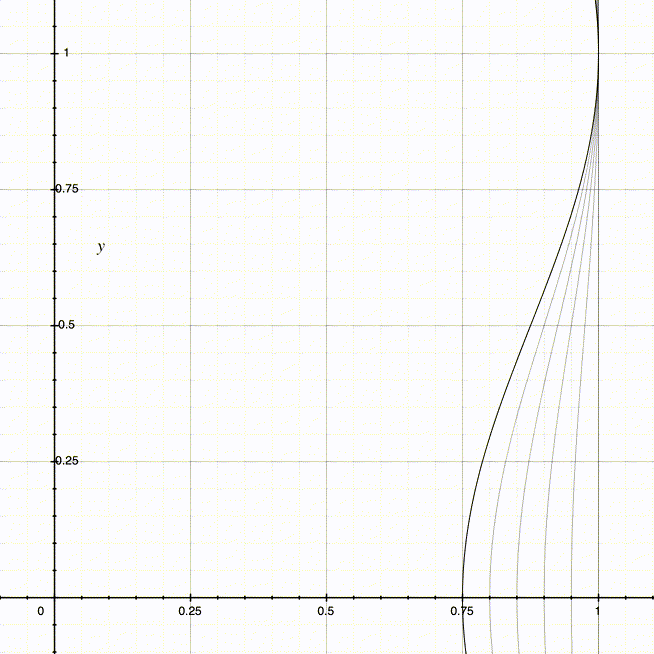
得到左右两侧曲线对应的函数后，就能很方便地实现神奇效果中的底部收缩了。

底部收缩

假如底部收缩的持续时间为curve_animation_duration，左侧曲线最终的值域最大值为left_max_end，右侧曲线最终的值域最小值为right_min_end，那么，根据时间（u_time）的不断增加，可以得到曲线演变的进度：

float curve_animation_progress = clamp(u_time / curve_animation_duration, 0.0, 1.0);

根据曲线演变进度，可以得到当前左侧曲线的值域最大值和当前右侧曲线的值域最小值：

float left_max = curve_animation_progress * left_max_end;
float right_min = 1.0 - curve_animation_progress * (1.0 - right_min_end);

进而计算出左右曲线各自的A、D：

// 左侧曲线：A * sin(π * y + π * 0.5) + D
// D - A = 0
// D + A = max
float leftD = left_max / 2.0;
float leftA = leftD;
float left = leftA * sin(pi * v_texcoord.y + pi * 0.5) + leftD;

// 右侧曲线：A * sin(π * y + π * 0.5) + D
// D - A = min
// D + A = 1
float rightD = (right_min + 1.0) / 2.0;
float rightA = 1.0 - rightD;
float right = rightA * sin(pi * v_texcoord.y - pi * 0.5) + rightD;

使用这样的纹理图片：

对其进行采样：

gl_FragColor = texture2D(u_texture_0, vec2((v_texcoord.x - left) / (right - left), v_texcoord.y));
// 左右透明
if (v_texcoord.x < left || v_texcoord.x > right) {
    gl_FragColor = vec4(0.0);
}

就可以得到这样的效果：

向下吸收

假如向下吸收的持续时间为translation_animation_duration，那么向下吸收的进度就是：

float translation_animation_progress = clamp((u_time - curve_animation_duration) / translation_animation_duration, 0.0, 1.0);

向下移动：

gl_FragColor = texture2D(u_texture_0, vec2((v_texcoord.x - left) / (right - left), v_texcoord.y + translation_animation_progress));
// 左右透明
if (v_texcoord.x < left || v_texcoord.x > right) {
    gl_FragColor = vec4(0.0);
}
// 顶部透明
if (v_texcoord.y + translation_animation_progress > 1.0) {
    gl_FragColor = vec4(0.0);
}

最终效果：

结束语

神奇效果还可以通过修改顶点来实现，不过，这种方式需要较多的顶点，才能让曲线足够光滑。

而通过修改采样时所使用的纹理坐标实现的神奇效果，并不需要那么多顶点。