使用位逻辑运算实现位向量
使用位逻辑运算实现位向量
解答《编程珠玑》中相关习题时的一些思考。
假定,我们需要使用X个类型为type的整数来创建一个至少包含N个比特位的位向量,那么,计算出的X就是:
int X = (int)ceil(N * 1.0 / (sizeof(type) * 8))
通过这些整数,形成一个数组,就能构建出了我们需要的位向量:
type bit_vector[X]
如果要对索引位置为i的比特位进行操作,就需要知道该比特位是哪个整数中的哪个比特位,因此需要处理两个小任务:
- 查找整数
- 查找整数中的比特位
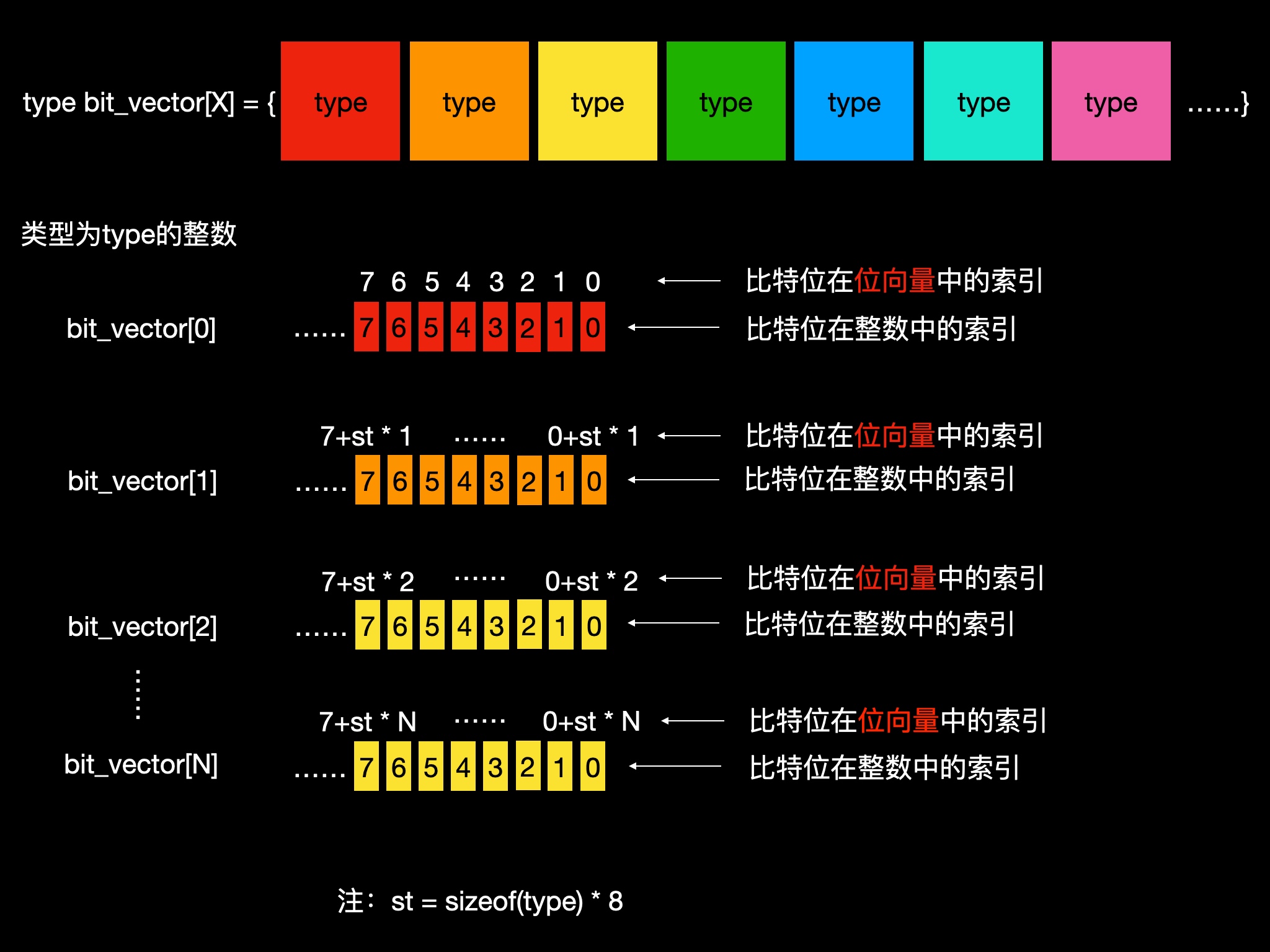
查找整数
查找整数,也即定位到该比特位所在的整数。
很明显,该整数在bit_vector中的索引N为:i / st,也即i >> log2(st)
这里,我们将log2(st)记为shift:
shift = log2(st)
因此,N = i >> shift。
使用不同的整数类型时,所对应的shift如下:
| 整数类型 | shift |
|---|---|
| uint8_t | 3 |
| uint16_t | 4 |
| uint32_t | 5 |
| uint64_t | 6 |
查找整数中的比特位
该比特位在整数bit_vector[N]中的索引是i % st,也即i - (i / st * st),使用位逻辑运算就是i - ((i >> log2(st)) << log2(st)),也即i - ((i >> shift) << shift)。
其中的(i >> shift) << shift,也就是将i的低shift位,置为0。示例:

所以,i - ((i >> shift) << shift)就表示保留i的低shift位的值。示例:
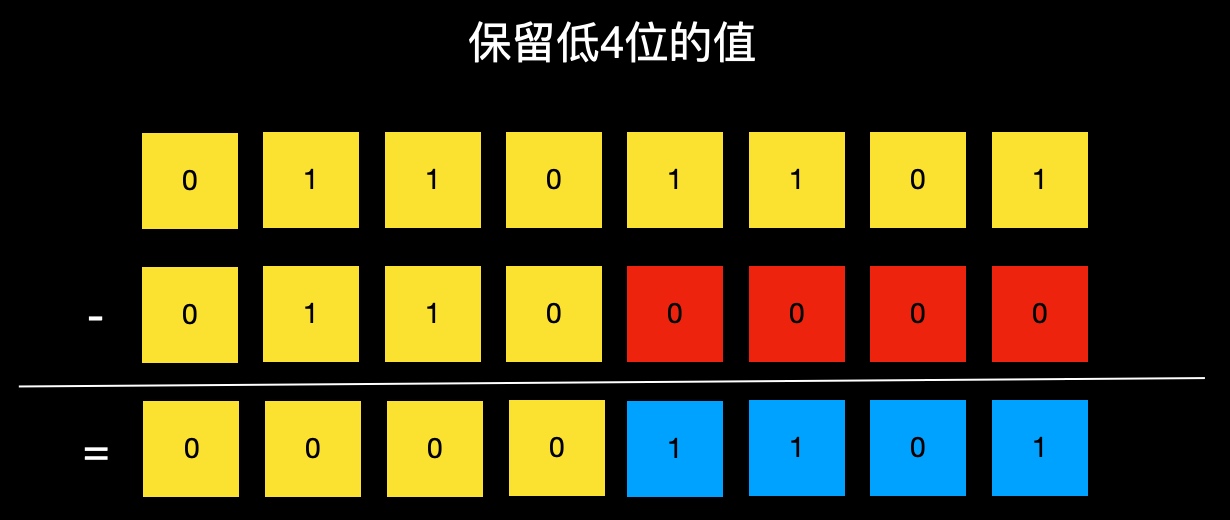
使用位逻辑运算实现低shift位的保留时,我们需要用到一个低shift位均为1而其他位均为0的整数,让其与i进行&运算。
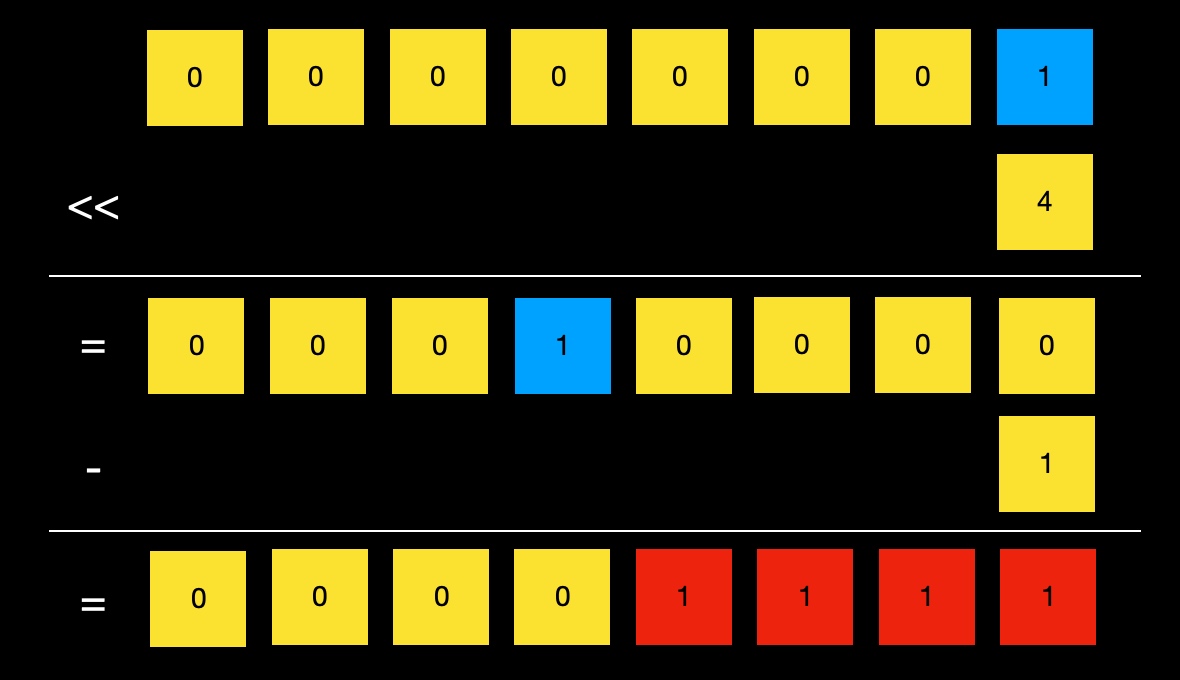
低shift位均为1而其他位均为0的整数,也即((1 << shift) - 1),我们将其记为mask:
mask = ((1 << shift) - 1)
使用mask实现低位保留:
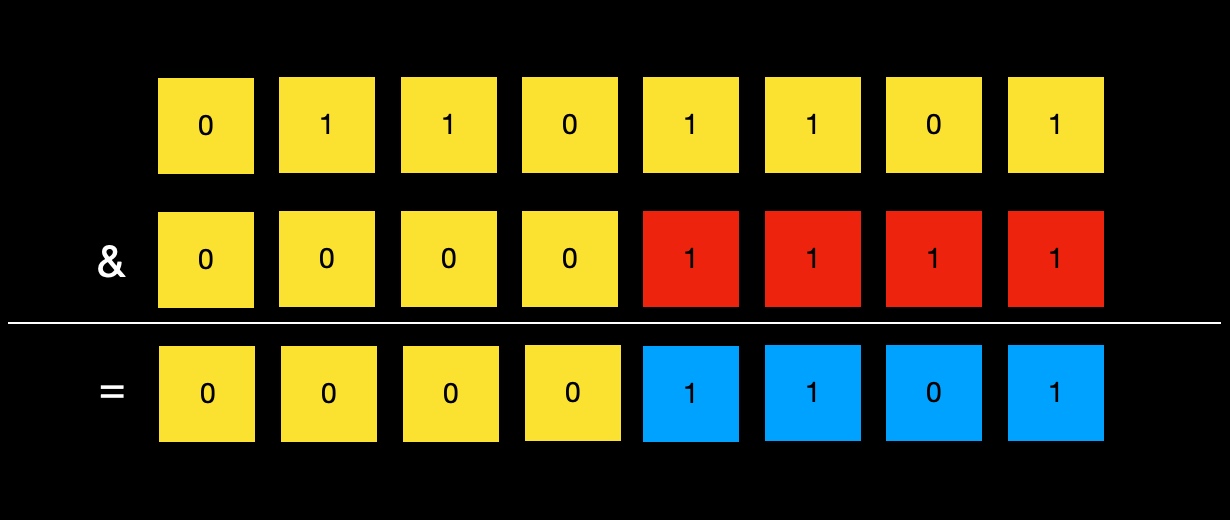
前面提到shift = log2(st),因此((1 << shift) - 1)就是st - 1。
使用不同的整数类型时,所对应的mask如下:
| 整数类型 | mask |
|---|---|
| uint8_t | 7(0x07) |
| uint16_t | 15(0x0F) |
| uint32_t | 31(0x1F) |
| uint64_t | 63(0x3F) |
最终,该比特位在整数bit_vector[i >> shift]中的索引i - ((i >> shift) << shift)可以用i & mask表示:
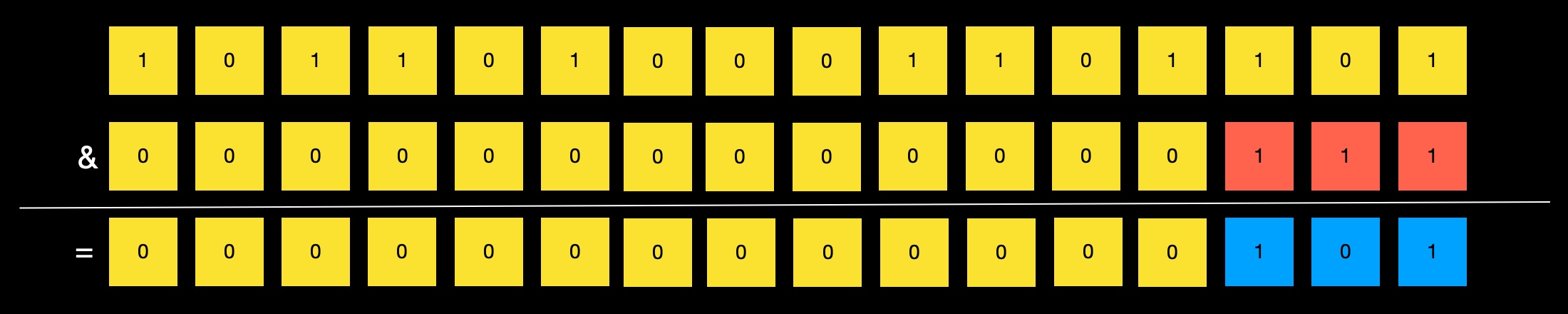
当对位向量中索引为i的比特位进行设置、清除、测试时,就可以用bit_vector[i >> shift]与(1 << (i & mask))进行位逻辑运算实现这些操作。
设置:
1 | |
清除:
1 | |
测试:
1 | |